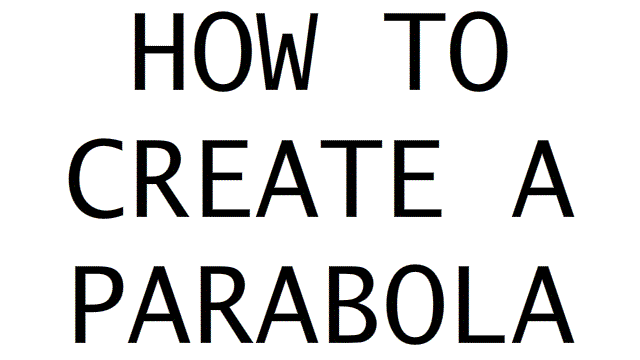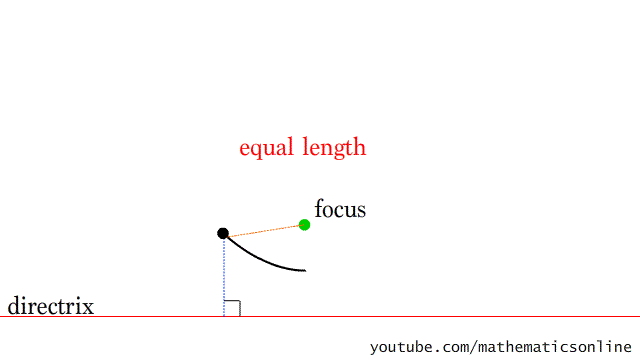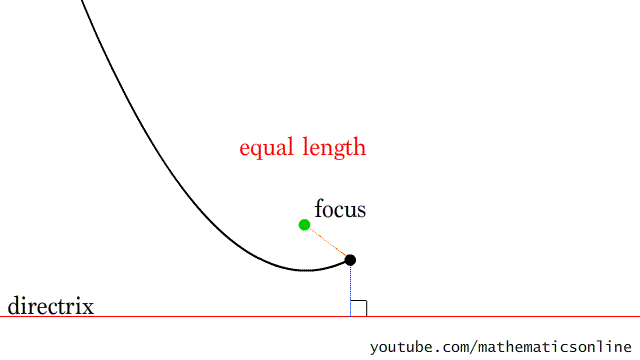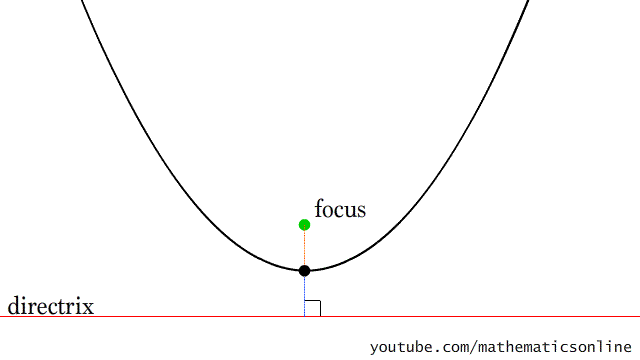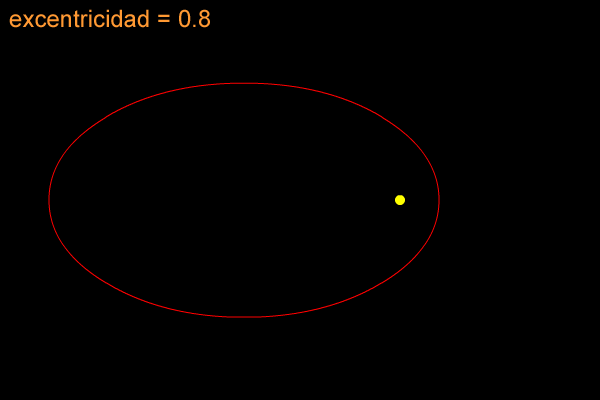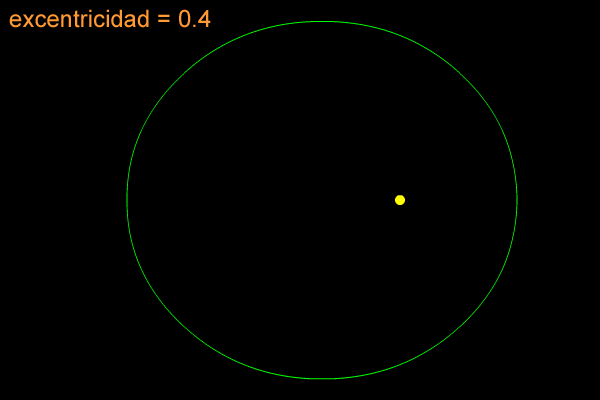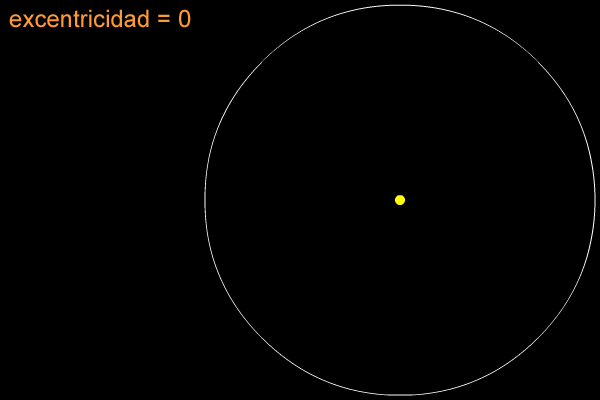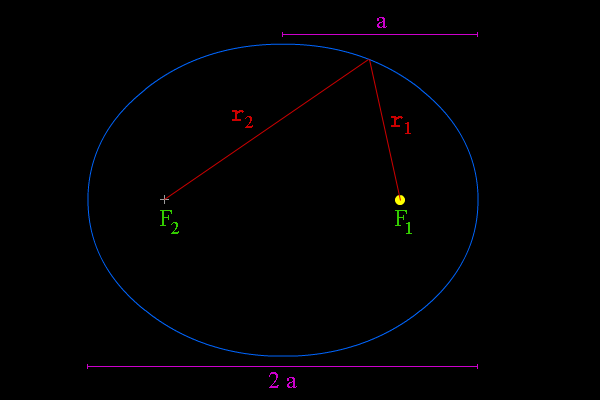
ECUACIÓN, ELEMENTOS Y GRÁFICA DE LA ELIPSE CON CENTRO EN EL ORIGEN

Hola chicos, aquí les dejo un video que les será de utilidad para resolver los ejercicios que se muestran más adelante. 

Saludos

LA ELIPSE Y SUS ELEMENTOS

TRABAJO FINAL

El trabajo final de la materia consiste en realizar una exposición de "Arte con hilos tensados" con figuras formadas por parábolas

ESPECIFICACIONES:

• La figura que se forme es de libre elección por los alumnos.
• La figura debe contener al menos 3 figuras cónicas (circuncerencias, parábolas o elipses) formadas por los hilos.
• El tamaño del cuadro o rectángulo donde formen la figura, no debe ser menor a 30cm de lado.
• El trabajo puede realizarse de manera individual, en parejas o en equipos de máximo 3 personas.
• FECHA DE ENTREGA: LUNES 18 DE DICIEMBRE
• El trabajo se evaluará bajo la siguiente escala:

 

Bachilleres UGM de Orizaba

ESCALA DE RANGO PARA EVALUAR FIGURAS DE HILOS TENSADOS

NOMBRE DEL ALUMNO: ____________________________________________________________ 

                                                                    SEMESTRE: ____________      FECHA:______________

                                                      

ESCALA DE VALORACIÓN (ESTIMACIÓN) 0% Nulo     1% Deficiente      3% Aceptable      4% Bueno      5%Excelente
No.	Indicador	Estimación	Ponderación	Puntaje obtenido
1	Entrega su trabajo bien terminado.		0.3
2	El trabajo es prolijo y detallado (No está hecho a la carrera y sin cuidado)		0.3
3	Los elementos están cuidadosamente asegurados al fondo		0.2
4	No hay marcas, rayones o manchas, nada cuelga de los bordes.		0.2
5	La figura presentada refleja un excepcional grado de creatividad del estudiante en su creación y/o exhibición.		0.4
6	Excepcionalmente bien diseñada, ordenada y atractiva		0.3
7	Para formar la figura se utilizan al menos 3 figuras cónicas (circunferencia, parábolas o elipses)		0.3
			TOTAL

                                                      

EVALUADOR: _____________________________________________________________________________________

A continuación se presentan algunos videos y figuras como muestra.

CLIC PARA MAS RECURSOS

PARÁBOLA CON CENTRO FUERA DEL ORIGEN Y SUS APLICACIONES

APRENDE MÁS SOBRE LA PARÁBOLA

Entra al siguiente enlace para seguir aprendiendo acerca de las parábolas

P A R A B O L A S➥

ELEMENTOS DE LA PARÁBOLA CON CENTRO EN EL ORIGEN, A PARTIR DE SU ECUACIÓN

ECUACIÓN Y TRAZO DE LA PARÁBOLA CON CENTRO EN EL ORIGEN

ECUACIÓN DE LA CIRCUNFERENCIA QUE PASA POR 3 PUNTOS

ECUACIÓN GENERAL DE LA CIRCUNFERENCIA

ECUACIÓN DE LA CIRCUNFERENCIA CON CENTRO Y RADIO DADOS

EJERCICIOS DE ECUACIÓN DE LA CIRCUNFERENCIA CON CENTRO EN EL ORIGEN

ECUACIÓN DE LA CIRCUNFERENCIA CON CENTRO EN EL ORIGEN

ELEMENTOS Y ECUACIONES DE LA CIRCUNFERENCIA

DISTANCIA DE UN PUNTO A UNA RECTA Y DISTANCIA ENTRE DOS RECTAS

ECUACIÓN GENERAL DE LA RECTA

GRÁFICA DE UNA RECTA A PARTIR DE LA ECUACIÓN PENDIENTE Y ORDENADA AL ORIGEN

ECUACIONES DE LA RECTA

CASO 1: Dados dos puntos

Utilizamos la forma punto-pendiente:   y - y1 = m (x - x1)
Para obtener:      1. Ecuación de la recta en la forma Pendiente y ordenada al origen    y = mx + b
                          2. Ecuación de la recta en su forma General    Ax + By + C = 0

Paso 1: Con los dos puntos dados calculamos la pendiente m
Paso 2: Sustituimos la pendiente y el punto P(x1, y1) en la Ecuación punto-pendiente
Paso 3: Despejamos y para obtener la ecuación en su forma Pendiente y Ordenada al Origen
Paso 4: Igualamos la ecuación anterior con cero para obtener la Ecuación General




CASO 2: Dados la pendiente y un punto

Utilizamos la forma punto-pendiente:   y - y1 = m (x - x1)
Para obtener:      1. Ecuación de la recta en la forma Pendiente y ordenada al origen    y = mx + b
                          2. Ecuación de la recta en su forma General    Ax + By + C = 0

Paso 1: Con los dos puntos dados calculamos la pendiente m  Omitimos este paso
Paso 1: Sustituimos la pendiente y el punto P(x1, y1) en la Ecuación punto-pendiente
Paso 2: Despejamos y para obtener la ecuación en su forma Pendiente y Ordenada al Origen
Paso 3: Igualamos la ecuación anterior con cero para obtener la Ecuación General

IMPORTANTE:  Poner especial atención en el manejo de los signos


Nota: En el video anterior no realizan el último paso, sin embargo, es el mismo procedimiento del primer video

CASO 3: Dados la pendiente y la ordenada al origen

Utilizamos directamente la Ecuación pendiente y ordenada el origen:  y = mx + b
Para obtener:     1. Ecuación de la recta en su forma General    Ax + By + C = 0

Paso 1: Con los dos puntos dados calculamos la pendiente m  Omitimos este paso
Paso 1: Sust. la m y el punto P(x1, y1) en la Ec. punto-pendiente Omitimos este paso
Paso 1: Sustituimos la pendiente m y el valor de la ordenada al origen (b) directamente en la ecuación en su  forma Pendiente y Ordenada al Origen
Paso 2: Igualamos la ecuación anterior con cero para obtener la Ecuación General

Nota: El valor de la ordenada al origen b es el punto donde la recta intersecta al eje y

ECUACIÓN DE LA RECTA COMO MODELO MATEMÁTICO

PARALELISMO Y PERPENDICULARIDAD

PENDIENTE DE UNA RECTA

RAZÓN DE UN SEGMENTO DE RECTA

PERÍMETROS Y ÁREAS EN EL PLANO CARTESIANO